Binary Number System
In these lessons we shall learn the binary number system and how to convert between binary and decimal numbers.
Related Pages
Number System
In a binary number (or base two) system, we use only two digits: 0 and 1.
The following diagrams show the place values for binary numbers and how to convert from binary to decimal.
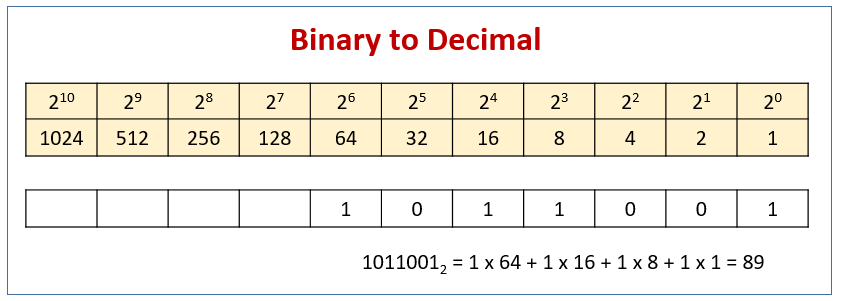
Convert From Binary To Decimal
Like base ten numbers, we can determine the value of a base two number by placing each digit in its respective place value, then writing its expanded notation.
Example:
Find the value of each of the following binary numbers, giving the values in decimal numbers:
a) 1012
b) 10112
c) 101012
Solution:
a)
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 |
1012 = 1 × 22 + 0 × 21 + 1 × 20
= 4 + 0 + 1
= 510
b)
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 1 |
10112 = 1 × 23 + 0 × 22 + 1 × 21 + 1 × 20
= 8 + 0 + 2 + 1
= 1110
c)
| 24 | 23 | 22 | 21 | 20 |
| 1 | 0 | 1 | 0 | 1 |
01012 = 1 × 24 + 0 × 23 + 1 × 22 + 0 × 21 + 1 × 20
= 16 + 0 + 4 + 0 + 1
= 2110
How To Convert Binary To Decimal?
Convert From Decimal To Binary
We can convert a decimal number into a binary number by repeatedly dividing the base ten number by two. Then, write the remainders from the bottom to the top as the answer:
Example:
Write each of the following base ten numbers as a binary number:
a) 510
b) 7810
Solution:
a)
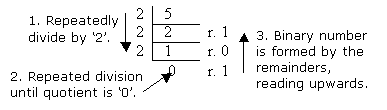
510 = 1012
b)
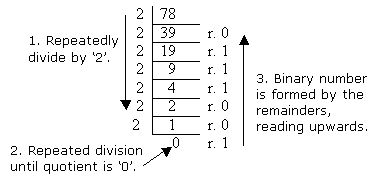
7810 = 10011102
Base 10 to Base 2 (Decimal to Binary) Conversion
A demonstration of the repeated divide by 2 method for converting numbers from base 10 (or decimal)
into base 2 (or binary) form.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.