Calculus - Area under a Curve
In these lessons, we will learn how to use integrals (or integration) to find the areas under the curves defined by the graphs of functions. We also learn how to use integrals to find areas between the graphs of two functions.
Related Pages
Integral Calculus
Calculus: Integration
Calculus: Derivatives
Calculus Lessons
We have also included calculators and tools that can help you calculate the area under a curve and area between two curves.
Formula For Area Bounded By Curves (Using Definite Integrals)
The Area A of the region bounded by the curves y = f(x), y = g(x) and the lines x = a, x = b, where f and g are continuous f(x) ≥ g(x) for all x in [a, b] is
![]()
The following diagrams illustrate area under a curve and area between two curves. Scroll down the page for examples and solutions.
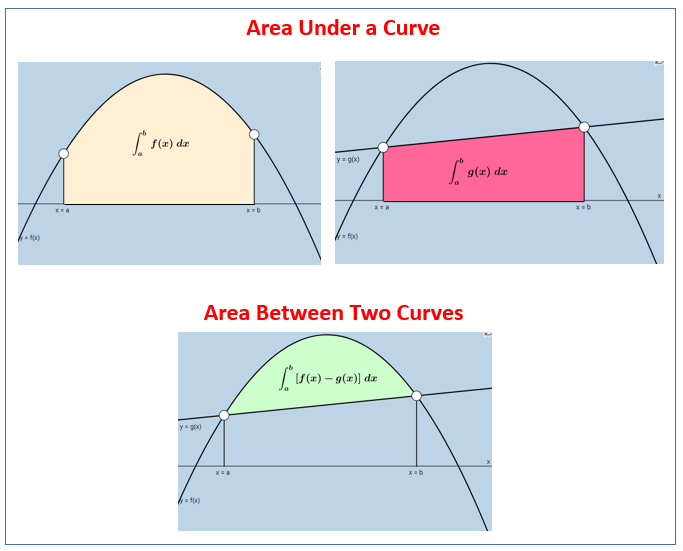
Example:
Find the area of the region bounded above by y = x2 + 1, bounded below by y = x,
and bounded on the sides by x = 0 and x = 1.
Solution:
The upper boundary curve is y = x2 + 1 and the lower boundary curve is y = x.
Using the formula for area bounded by curves,
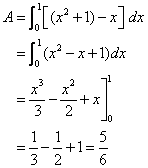
How to find the Area between Curves?
Example:
Find the area between the two curves y = x2 and y = 2x – x2.
Solution:
Step 1: Find the points of intersection of the two parabolas
by solving the equations simultaneously.
x2 = 2x – x2
2x2 – 2x = 0
2x(x – 1) = 0
x = 0 or 1
The points of intersection are (0, 0) and (1, 1)
Step 2: Find the area between x = 0 and x = 1
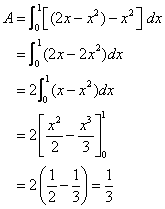
How to use the Area Under a Curve to approximate the definite integral?
Example:
Approximate the area under the curve f(x) = x2 (i.e. the area between y = x2 and
y = 0) from x = 1 to 3. Use n = 4 rectangles.
How to find the area under a curve using integration, step by step, example
Example:
Find the area bounded by the curves y = x2 - 6x + 9 and y = x + 3.
How to use integration to determine the area under a curve?
A parabola is drawn such that it intersects the x-axis. The x-intercepts are determined so that the area can be calculated.
Example:
Calculate the area enclosed by the curve y = 2x - x2 and the x-axis.
How to use Definite Integrals to find Area Under a Curve?
Use the following Definite Integral Calculator to find the Area under a curve.
Enter the function, lower bound and upper bound.
How to Find Areas Between Curves?
Example:
Find the area bounded by the curves y = x2 - 4x and y = 2x.
How to find area between curves by Integrating with Respect to y.
Example:
Find the area bounded by the curves x = y3 - y and x = 1 - y4.
Use the following Area between Curves Calculator to show you the steps and to check your answers.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.