AP Calculus BC 2015 Questions and Answers
Questions and Worked Solutions for AP Calculus BC 2015.
AP Calculus BC 2015 Free Response Questions - Complete Paper (pdf)
AP Calculus BC 2015 Free Response Question 1
- The rate at which rainwater flows into a drainpipe is modeled by the function R, where
 cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0. (a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?
cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0. (a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?
(b) Is the amount of water in the pipe increasing or decreasing at time t 3 hours? Give a reason for your answer.
(c) At what time t, 0 ≤ t ≤ 8, is the amount of water in the pipe at a minimum? Justify your answer.
(d) The pipe can hold 50 cubic feet of water before overflowing. For t > 8, water continues to flow into and out of the pipe at the given rates until the pipe begins to overflow. Write, but do not solve, an equation involving one or more integrals that gives the time w when the pipe will begin to overflow.
AP Calculus BC 2015 Free Response Question 2
2. At time t ≥ 0, a particle moving along a curve in the xy-plane has position (x(t),y(t)) with velocity vector v(t) = (cos(t2), e0.5t). At t = 1, the particle is at the point (3, 5).
(a) Find the x-coordinate of the position of the particle at time t = 2.
(b) For 0 < t < 1, there is a point on the curve at which the line tangent to the curve has a slope of 2.
At what time is the object at that point?
(c) Find the time at which the speed of the particle is 3.
(d) Find the total distance traveled by the particle from time t = 0 to time t = 1
AP Calculus BC 2015 Free Response Question 3

AP Calculus BC 2015 Free Response Question 4

AP Calculus BC 2015 Free Response Question 5

AP Calculus BC 2015 Free Response Question 6

Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
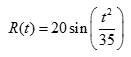 cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0. (a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?
cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0. (a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?