AP Calculus AB 2015 Questions and Answers
Related Pages
AP Calculus AB 2016 Exam
AP Calculus AB 2018 Exam
AP Calculus AB 2017 Exam
Calculus Lessons
Questions and Worked Solutions for AP Calculus AB 2015
AP Calculus AB 2015 Free Response Questions - Complete Paper (pdf)
AP Calculus AB 2015 Free Response Question 1
- The rate at which rainwater flows into a drainpipe is modeled by the function R, where
 cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0. (a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?
cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0. (a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?
(b) Is the amount of water in the pipe increasing or decreasing at time t 3 hours? Give a reason for your answer.
(c) At what time t, 0 ≤ t ≤ 8, is the amount of water in the pipe at a minimum? Justify your answer.
(d) The pipe can hold 50 cubic feet of water before overflowing. For t > 8, water continues to flow into and out of the pipe at the given rates until the pipe begins to overflow. Write, but do not solve, an equation involving one or more integrals that gives the time w when the pipe will begin to overflow.
AP Calculus AB 2015 Free Response Question 2
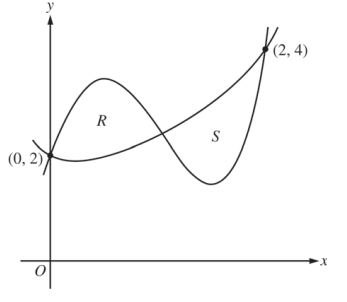
- Let f and g be the functions defined by f(x) = 1+ x + ex2 - 2x and g(x) = x4 - 6.5x2 + 6x + 2. Let R and S be the two regions enclosed by the graphs of f and g shown in the figure above.
(a) Find the sum of the areas of regions R and S.
(b) Region S is the base of a solid whose cross sections perpendicular to the x-axis are squares. Find the volume of the solid.
(c) Let h be the vertical distance between the graphs of f and g in region S. Find the rate at which h changes with respect to x when x = 1.8.
AP Calculus AB 2015 Free Response Question 3

AP Calculus AB 2015 Free Response Question 4

AP Calculus AB 2015 Free Response Question 5
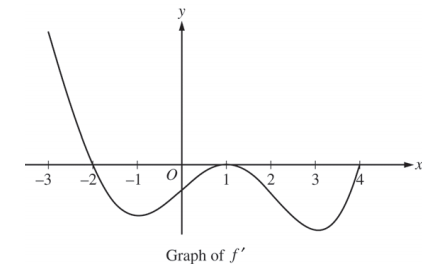
- The figure above shows the graph of f', the derivative of a twice-differentiable function f, on the interval [-3,4]. The graph of f' has horizontal tangents at x = -1, x = 1, and x = 3. The areas of the regions bounded by the x-axis and the graph of f' on the intervals [-2,1] and [1,4] are 9 and 12, respectively.
(a) Find all x-coordinates at which f has a relative maximum. Give a reason for your answer.
(b) On what open intervals contained in -3 < x < 4 is the graph of f both concave down and decreasing?
Give a reason for your answer.
(c) Find the x-coordinates of all points of inflection for the graph of f. Give a reason for your answer.
(d) Given that f(1) = 3, write an expression for f(x) that involves an integral. Find f(4) and f(-2).
AP Calculus AB 2015 Free Response Question 6

Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
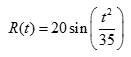 cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0. (a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?
cubic feet per hour, t is measured in hours, and 0 ≤ t ≤ 8. The pipe is partially blocked, allowing water to drain out the other end of the pipe at a rate modeled by D(t) = -0.04t3 + 0.4t2 + 0.96t cubic feet per hour, for 0 ≤ t ≤ 8. There are 30 cubic feet of water in the pipe at time t = 0. (a) How many cubic feet of rainwater flow into the pipe during the 8-hour time interval 0 ≤ t ≤ 8?