45-45-90 Right Triangles
In these lessons, we will learn
- the special right triangle called the 45°-45°-90° triangle
- how to solve problems involving the 45°-45°-90° right triangle
Related Pages
30-60-90 Right Triangle
Other Special Right Triangles
More Geometry Lessons
Recognizing special right triangles in geometry can provide a shortcut when answering some questions. A special right triangle is a right triangle whose sides are in a particular ratio. You can also use the Pythagorean theorem formula, but if you can see that it is a special triangle it can save you some calculations.
What is a 45-45-90 Triangle? {#45-45-90triangles}
A 45-45-90 triangle is a special right triangle whose angles are 45°, 45° and 90°. The
lengths of the sides of a 45-45-90 triangle are in the ratio of 1:1:√2.
The following diagram shows a 45-45-90 triangle and the ratio of its sides. Scroll down the page for more examples and solutions using the 45-45-90 triangle.
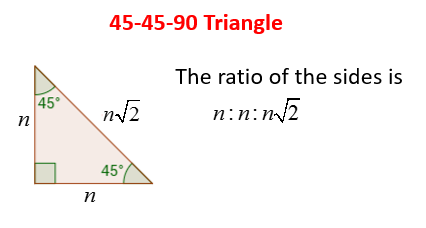
Note that a 45-45-90 triangle is an isosceles right triangle. It is also sometimes called a 45-45 right triangle.
A right triangle with two sides of equal lengths is a 45-45-90 triangle.
You can also recognize a 45-45-90 triangle by the angles. As long as you know that one of the angles in the right-angle triangle is 45° then it must be a 45-45-90 special right triangle.
A right triangle with a 45° angle must be a 45-45-90 special right triangle.
How to solve problems with 45-45-90 triangles?
Example 1:
Find the length of the hypotenuse of a right triangle if the lengths of the other two sides are both 3 inches.
Solution:
Step 1: This is a right triangle with two equal sides so it
must be a 45-45-90 triangle.
Step 2: You are given that the both the sides are 3. If the first and second value of the ratio n:n:n√2 is 3 then the length of the third side is 3√2
Answer: The length of the hypotenuse is 3√2 inches.
Example 2:
Find the lengths of the other two sides of a right triangle if the length of the hypotenuse
is 4√2 inches and one of the angles is 45°.
Solution:
Step 1: This is a right triangle with a 45° so it must be
a 45-45-90 triangle.
Step 2: You are given that the hypotenuse is 4√2. If the third value of the ratio n:n:n√2 is 4√2 then the lengths of the other two sides must 4.
Answer: The lengths of the two sides are both 4 inches.
Videos
The following videos show more examples of 45-45-90 triangles.
How to find the length of a leg or hypotenuse in a 45-45-90 triangle using the Pythagorean Theorem and then derive the ratio between the length of a leg and the hypotenuse?
This video gives an introduction to the 45-45-90 triangles and shows how to derive the
ratio between the lengths of legs and the hypotenuse.
How to solve a 45-45-90 triangle given the length of one side by using the ratio?
Special Right Triangles in Geometry: 45-45-90 and 30-60-90
This video discusses two special right triangles, how to derive the formulas to find the lengths of the sides of the triangles by knowing the length of one side, and then does a few examples using them.
Example problems of finding the sides of a 45-45-90 triangle with answer in simplest radical form.
Try the free Mathway calculator and
problem solver below to practice various math topics. Try the given examples, or type in your own
problem and check your answer with the step-by-step explanations.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.